THE ULTIMATE TOOL
FOR TRADERS
System Demo
Watch our automated scanners find explosive opportunities in the market!
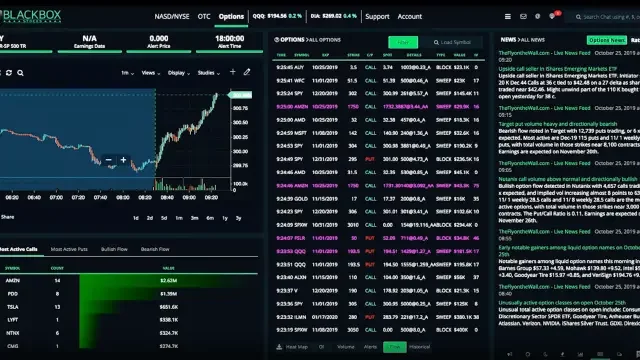
Option Flow Scanner
See how our options flow scanner allows you to follow the “smart money”!
System Demo
Options Flow


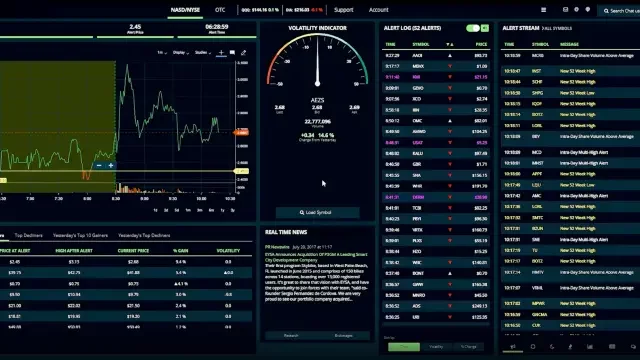
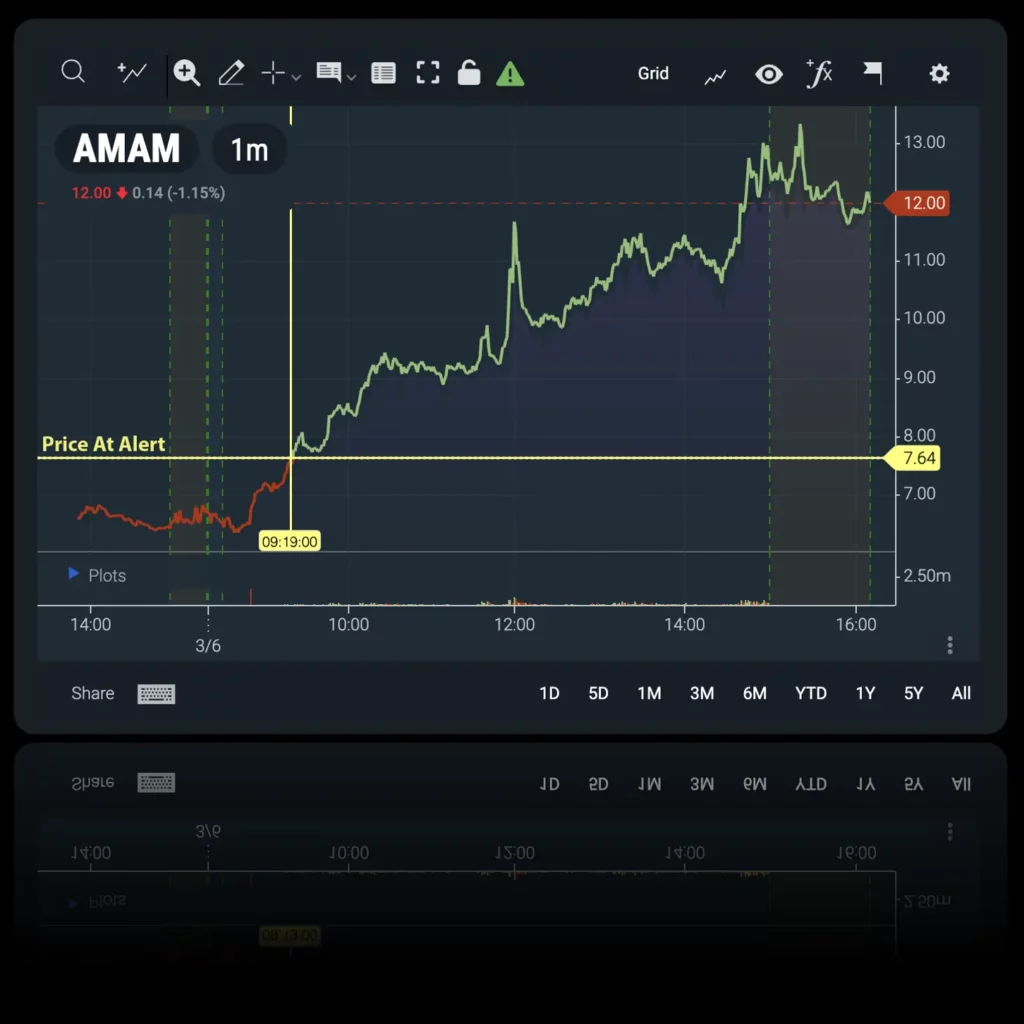
We are distinctly different than any other trading system on the market. Long before the market opens, our system scans the exchanges using proprietary algorithms to find the most active stocks. Our fully automated scanners then send you alerts to explosive opportunities in the market in real time. Once an alert is posted, you can click on the symbol and find out why that stock received an alert. Then use our advanced charting tools and proprietary volatility indicator to see which stocks are breaking out and posting the biggest gains.
Our system continuously scans the NASDAQ, New York Stock Exchange, CBOE and all other options markets analyzing over 8,000 stocks, and up to 900,000 options contracts multiple times per second. Our algorithms are similar to those used in extremely profitable ‘high frequency trading’ (HFT) strategies. We are here to level the playing field offering you technology that has too often been reserved for large financial firms, hedge funds, and the Wall Street elite.
Our Proprietary Features
Powerful Alerts
Our fully automated algorithm-based system scans over 11,000 stocks multiple times per second to find the most volatile stocks and alert you to the biggest moves in the market before they occur.
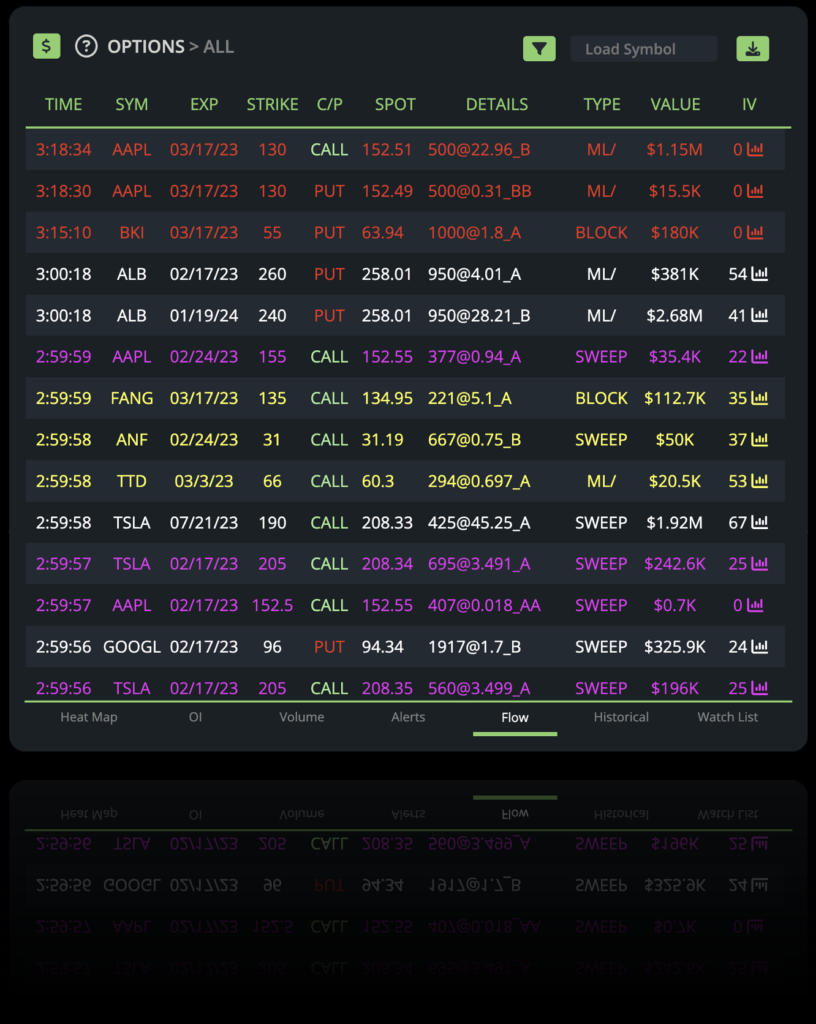
Options Flow
The BlackBox Options Flow Scanner tracks large aggressive buying activity in specific options contracts. Unusual options activity moves markets. Our proprietary logic gives our members a window into Wall Street to follow the smart money. This information is gold for options traders!
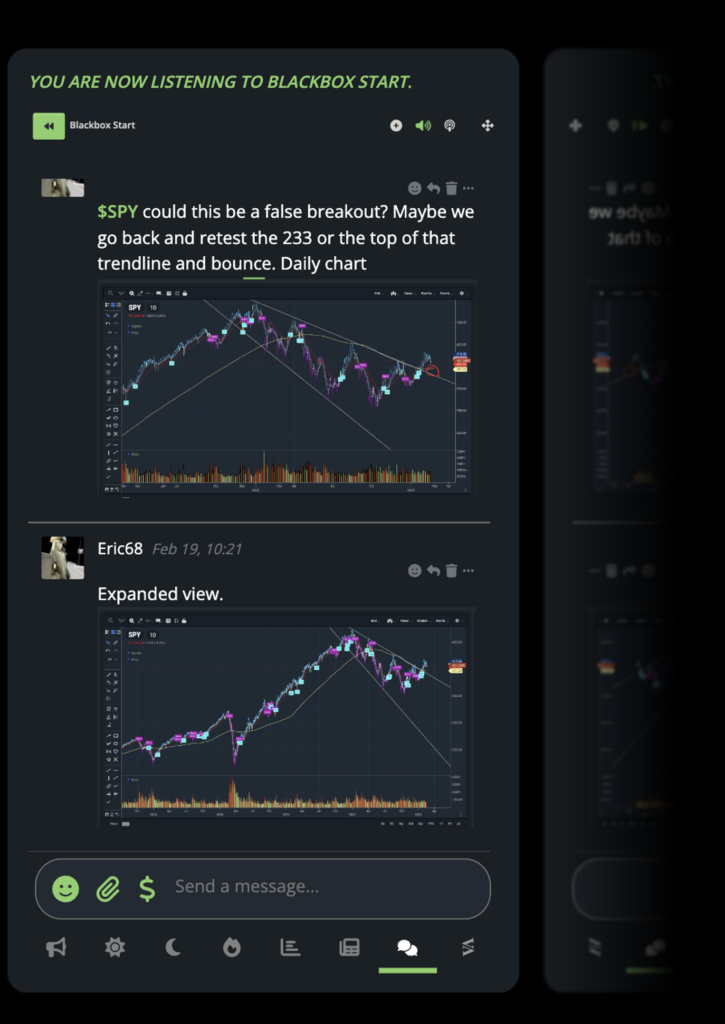
Trading Community
No one trades alone. Chat directly with experienced and new traders alike on the Blackbox platform. There’s no need to waste precious time switching between platforms and tabs.
- Listen to Live Channels
- Collaborate and Share Ideas
- Interact with Seasoned Veterans in a Team Environment
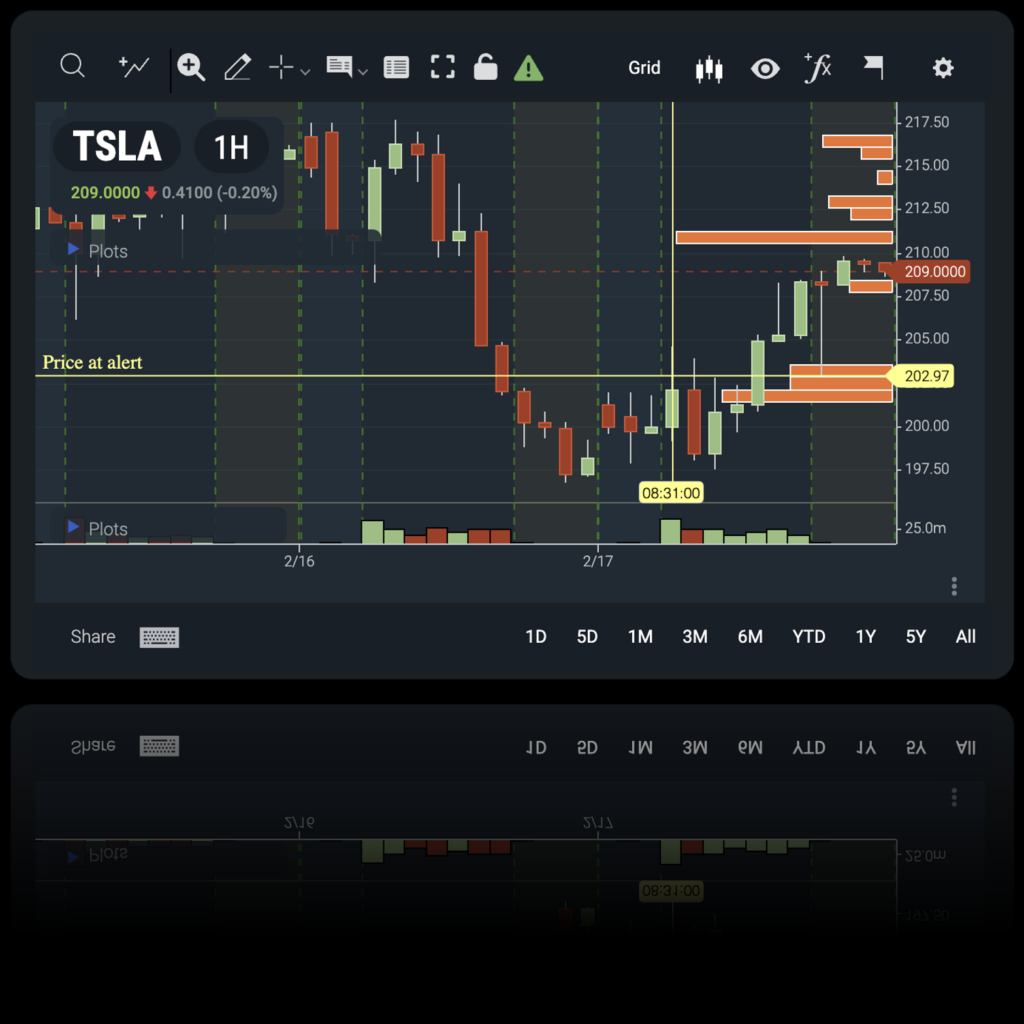
Dark Pool
Dark Pools are private exchanges where financial institutions conduct large block trades outside of the public markets. Our Dark Pool scanner provides our members with real-time insight into what is happening in these mysterious private exchanges.
Live Courses
Live Courses
We offer a comprehensive curriculum of courses free of cost to all BlackBox members. We teach you how to become a top trader with our platform.
We offer a comprehensive curriculum of live and recorded courses free of charge to all BlackBox members. We teach you how to become a top trader with our platform.
Join Team Blackbox
A Worldwide Community








































Join Our Discord!
Track Our Top Alerts
See our Top Gainers from the previous day. Our alert log finds the biggest profit opportunities in the market!
| Symbol | Price at Alert | High After Alert | Change | % Potential Gain |
|---|---|---|---|---|
| EZGO | $2.02 | $3.8 | $1.78 | 88.12% |
| INDO | $3.26 | $5.94 | $2.68 | 82.21% |
| TPET | $0.4 | $0.69 | $0.29 | 73.48% |
| HNRA | $2.74 | $4 | $1.26 | 45.99% |
| MNDR | $11.25 | $16 | $4.75 | 42.22% |
| HUSA | $1.9 | $2.58 | $0.68 | 35.65% |
| Symbol | Strike | Call / Put | Price at Alert | Daily High | Percent to High |
|---|---|---|---|---|---|
| ACB | 7 | CALL | $0.15 | $0.83 | 460.81% |
| ACB | 7 | CALL | $0.15 | $0.83 | 460.81% |
| NVDA | 880 | PUT | $1.28 | $5.7 | 345.31% |
| AAPL | 175 | CALL | $0.82 | $3.5 | 326.83% |
| AAPL | 178 | CALL | $0.37 | $1.57 | 320.91% |
| AAPL | 178 | PUT | $1.04 | $2.73 | 162.75% |
*This data is updated daily to allow you to track our system’s performance.
Our Team Traders
These are our top traders and leaders of our community. Listen to our Team Traders live in our members channels daily to find your winning trades!
Kang’s background spans 18+ years in banking and finance. After joining Blackbox in April 2018, he was able to ramp up quickly by leveraging the platform features and the experience of our diverse trading community.
Kang shares his knowledge through his technical analysis daily in our live options trading room.
Maria became a member of BlackBoxStocks in October 2016 and quickly became a well-known member of the Blackbox trading community. In 2017, Maria joined the BlackBoxStocks team as a moderator in their online community.
Maria spends her days trading with the BlackBoxStocks community as well educating and mentoring BlackBoxStocks members. In addition, Maria actively promotes Blackbox on multiple social media platforms to showcase the unique proprietary features and benefits of the platform.
You can find her live in the Blackbox Start trade room helping the community build their account balance one trade at a time.
Taylor joined BlackBoxStocks as a member in 2018 and never looked back. Blackbox and its community were integral to Taylor’s success.
You can find Taylor live in our options trade room calling out actionable data and trades for the members.

Bender has been a full-time trader for many years. His uncanny knack for finding under the radar winners over the years has been exceptional, as has his desire to educate as he navigates the markets.
You will enjoy hearing Bender everyday live in our options room called Roadhouse.
You can find Teah on her live channel daily on Blackbox where she helps members with breakout and momentum trades on any stock priced above $1.00. Momentum trading is basically entering trades in the direction of a trend.

Our 5 Star Experience









Save with an Annual Subscription
All Inclusive Membership
OR
Start Your 7 Day Free Trial - No Risk
Our Brokerage Partners

Web API Integration COMING SOON.
Join BlackBox and receive the link to open a tastyworks account in our “Welcome Email.”
tastyworks, Inc. and BlackBoxStocks, Inc. are separate, unaffiliated companies and are not responsible for each other’s services and products.
$0.00 Commission on all Stock Trades
$1.00 Per Options Contract, No Ticket Fee
(Open only, $10 Max per leg)
*Must open with or have a minimum balance of $2,000.00 in your account to be eligible for these discounted rates. Below is the link for our members to sign up and receive the discounted rates if they open an account with $2,000.00 and are an active BlackBoxStocks member

Trade directly from our system using the new web API Integration.
Join BlackBox and we’ll email you the link to open a TradeStation account and receive the special discounted rate.
TradeStation, Inc. and BlackBoxStocks, Inc. are separate, unaffiliated companies and are not responsible for each other’s services and products.
$0.00 Commission on all Stock Trades
$0.35 Per Options Contract, No Ticket Fee
$0.75 Futures Minis
$0.25 Futures Micros
*Must open with or have a minimum balance of $2,000.00 in your account to be eligible for these discounted rates. Below is the link for our members to sign up and receive the discounted rates if they open an account with $2,000.00 and are an active BlackBoxStocks member



